I have been trying to do this online pattern generator using shading language.
Enter a formula: Example formulas to enter:Graphics, Game Development and Digital Art
Welcome to the enticing world of gaming and graphics.
Thursday, March 7, 2024
Create a Texture Online
Saturday, January 28, 2023
Sierpinski Gasket in an Android App
After making several apps which were not doing anything much but just to know the way android apps are created, sat down to create applications which might be a bit useful.
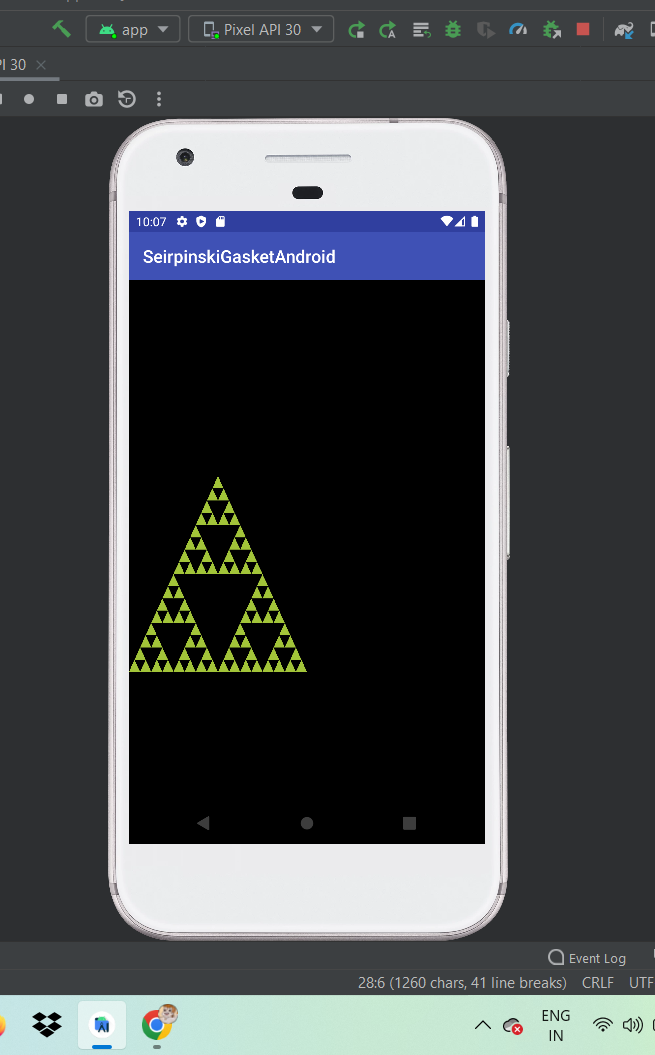
First of them, an android app that displays a sierpinski gasket.
Here is a snap:
This is the autogenerated MainActivity.java with a little modifications:
package com.example.mukesh.seirpinskigasketandroid;
import android.opengl.GLSurfaceView;
import android.support.v7.app.AppCompatActivity;
import android.os.Bundle;
public class MainActivity extends AppCompatActivity {
private GLSurfaceView mGLView;
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
mGLView = new MyGLSurfaceView(this);
setContentView(mGLView);
}
}
Next up the MyGLSurfaceView.java classpackage com.example.mukesh.seirpinskigasketandroid;
import android.content.Context;
import android.opengl.GLSurfaceView;
public class MyGLSurfaceView extends GLSurfaceView {
private final MyGLRenderer mRenderer;
public MyGLSurfaceView(Context context) {
super(context);
// Create an OpenGL ES 2.0 context
setEGLContextClientVersion(2);
mRenderer = new MyGLRenderer();
// Set the Renderer for drawing on the GLSurfaceView
setRenderer(mRenderer);
// Render the view only when there is a change in the drawing data
setRenderMode(GLSurfaceView.RENDERMODE_WHEN_DIRTY);
}
}
Next the MyGlRenderer.java classpackage com.example.mukesh.seirpinskigasketandroid;
import android.opengl.GLES20;
import android.opengl.GLSurfaceView;
import javax.microedition.khronos.egl.EGLConfig;
import javax.microedition.khronos.opengles.GL10;
public class MyGLRenderer implements GLSurfaceView.Renderer {
private Triangle mTriangle;
@Override
public void onSurfaceCreated(GL10 gl10, EGLConfig eglConfig) {
GLES20.glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
// initialize a triangle
mTriangle = new Triangle();
// initialize a square
}
@Override
public void onSurfaceChanged(GL10 gl10, int width, int height) {
GLES20.glViewport(0, 0, width, height);
}
@Override
public void onDrawFrame(GL10 gl10) {
GLES20.glClear(GLES20.GL_COLOR_BUFFER_BIT);
mTriangle.draw();
}
public static int loadShader(int type, String shaderCode){
// create a vertex shader type (GLES20.GL_VERTEX_SHADER)
// or a fragment shader type (GLES20.GL_FRAGMENT_SHADER)
int shader = GLES20.glCreateShader(type);
// add the source code to the shader and compile it
GLES20.glShaderSource(shader, shaderCode);
GLES20.glCompileShader(shader);
return shader;
}
}
Next is the Triangle.java class
package com.example.mukesh.seirpinskigasketandroid;
import android.opengl.GLES20;
import java.nio.ByteBuffer;
import java.nio.ByteOrder;
import java.nio.FloatBuffer;
public class Triangle {
private final int mProgram;
private FloatBuffer vertexBuffer;
// number of coordinates per vertex in this array
static final int COORDS_PER_VERTEX = 3;
static float triangleCoords[] = { // in counterclockwise order:
0.0f, 0.622008459f, 0.0f, // top
-0.5f, -0.311004243f, 0.0f, // bottom left
0.5f, -0.311004243f, 0.0f // bottom right
};
float v[][]={{-1.0f,-0.5f,0.0f},{1.0f,-0.5f,0.0f},
{0.0f,1.0f,0.0f}};
float colors[][]={{1.0f,0.0f,0.0f},{0.0f,1.0f,0.0f},{0.0f,0.0f,1.0f},{0.0f,0.0f,0.0f}};
int n=5;
int vc1=0;
// Set color with red, green, blue and alpha (opacity) values
float color[] = { 0.63671875f, 0.76953125f, 0.22265625f, 1.0f };
public Triangle() {
// initialize vertex byte buffer for shape coordinates
ByteBuffer bb = ByteBuffer.allocateDirect(
// (number of coordinate values * 4 bytes per float)
10000);
// use the device hardware's native byte order
bb.order(ByteOrder.nativeOrder());
// create a floating point buffer from the ByteBuffer
vertexBuffer = bb.asFloatBuffer();
// add the coordinates to the FloatBuffer
//vertexBuffer.put(triangleCoords);
// set the buffer to read the first coordinate
divide_tetra(vertexBuffer,v[0],v[1],v[2],n);
vertexBuffer.position(0);
int vertexShader = MyGLRenderer.loadShader(GLES20.GL_VERTEX_SHADER,
vertexShaderCode);
int fragmentShader = MyGLRenderer.loadShader(GLES20.GL_FRAGMENT_SHADER,
fragmentShaderCode);
// create empty OpenGL ES Program
mProgram = GLES20.glCreateProgram();
// add the vertex shader to program
GLES20.glAttachShader(mProgram, vertexShader);
// add the fragment shader to program
GLES20.glAttachShader(mProgram, fragmentShader);
// creates OpenGL ES program executables
GLES20.glLinkProgram(mProgram);
}
void triangle(FloatBuffer fb,float a[],float b[],float c[])
{
fb.put(a);
fb.put(b);
fb.put(c);
vc1++;
}
void divide_tetra(FloatBuffer fb,float a[],float b[],float c[],int m)
{
float v1[]=new float[3],v2[]=new float[3],v3[]=new float[3];
int j;
if(m>0)
{ /*compute three midpoints*/
for(j=0;j<3;j++)
v1[j]=(a[j]+b[j])/2;
for(j=0;j<3;j++)
v2[j]=(a[j]+c[j])/2;
for(j=0;j<3;j++)
v3[j]=(c[j]+b[j])/2;
divide_tetra(fb,a,v2,v1,m-1);
divide_tetra(fb,c,v3,v2,m-1);
divide_tetra(fb,b,v1,v3,m-1);
}
else
triangle(fb, a, b, c); //draw triangle at end of recursion//
}
private final String vertexShaderCode =
"attribute vec4 vPosition;" +
"void main() {" +
" gl_Position = vPosition;" +
"}";
private final String fragmentShaderCode =
"precision mediump float;" +
"uniform vec4 vColor;" +
"void main() {" +
" gl_FragColor = vColor;" +
"}";
private int mPositionHandle;
private int mColorHandle;
private final int vertexCount = triangleCoords.length / COORDS_PER_VERTEX;
private final int vertexStride = COORDS_PER_VERTEX *4; // 4 bytes per vertex
public void draw() {
// Add program to OpenGL ES environment
GLES20.glUseProgram(mProgram);
// get handle to vertex shader's vPosition member
mPositionHandle = GLES20.glGetAttribLocation(mProgram, "vPosition");
// Enable a handle to the triangle vertices
GLES20.glEnableVertexAttribArray(mPositionHandle);
// Prepare the triangle coordinate data
GLES20.glVertexAttribPointer(mPositionHandle, COORDS_PER_VERTEX,
GLES20.GL_FLOAT, false,
vertexStride, vertexBuffer);
// get handle to fragment shader's vColor member
mColorHandle = GLES20.glGetUniformLocation(mProgram, "vColor");
// Set color for drawing the triangle
GLES20.glUniform4fv(mColorHandle, 1, color, 0);
// Draw the triangle
GLES20.glDrawArrays(GLES20.GL_TRIANGLES, 0,vc1);
// Disable vertex array
GLES20.glDisableVertexAttribArray(mPositionHandle);
}
}
Several things need to be done majorly:
Creating the run/Debug configurations and selecting the emulator device.
This is how the output looks like:
for n=4 the triangle subdivision is upto 3 levels and here is how it looks like:
for n=3 the subdivisions are:
Thank you!!
https://github.com/bmkamath2000/mukBoApps/tree/main/SeirpinskiGasketAndroid
Thursday, December 2, 2021
Stupidest Project I had ever laid my hands on
I need to get this out and out pretty quickly.
If blogging is a way of venting ones frustrations then so be it. I thought why would people be interested in my rants and deduced that they might like reading it if I act Stupid and Dumb.
From my experiences as a rickety software writer, I have come to believe that there exists a class of projects that lie at the border between the possible and the impossible.
No extra points for failing in a software project. But see my teachers were making it a point to force me to write the purpose I was writing a code for at the start of the program.
It used to be like:
"WAP to display the first n fibonacci numbers in the fibonacci series"
I never questioned them and being an obedient student followed every bit of instruction given.
Now no one writes code that does nothing and its presumed that people are into coding to do useful stuff.
But I never found anything interesting or useful in the series we generated.
Not that it mattered as long as we got those elusive extra marks.
Coming to the main topic of this post:
THE most stupid project I have ever laid my hands on that seemed to be at the border of the possible/impossible is VISUAL PROGRAMMING
My advice to people dreaming of such things is to stop doing that and get real.
I in fact gave a seminar on this topic in my post graduation. Literature was hard to come by. There were classifications of programming languages. But not visual programming languages.
I hybridized literature that spoke about Programming by Example with some obscure software called Pygmalion. I also looked at some radically new ways of representing program execution and data.
I spoke on recording user actions as done in macros. I spoke of showing program actions by animation and representing data as visual elements such as boxes.
Finally when it came to implementation It never came to fruition. Post graduation is where you get your ideas tested and the feedback that I got from Dr. Dobbs journal editor can be summarized in one word:
"Interesting"
Would like some comments if it helps clarify.. Don't know what use this technology, if I may call it that, might be put to use in. In light of recent developments in AR/VR and HMD may be its got some real uses in program debugging or tools to represent program visually so that programming errors become evident. It could also help in cases where programmer needs help to visualize complex data structures.
Tuesday, November 23, 2021
Polyline Tweening in Javascript Canvas
Here is a link to google books for the said pages in the this book.
Monday, May 10, 2021
Can you create svg graphic from obj files
Saturday, December 5, 2020
Introduction to Three.js
Three.JS is a graphics framework/library that can render into canvas/svg/webgl contexts. The library has powerful capabilities to display complex 3D scenes with multiple models/camera/lights in it. I will demonstrate a program that rotates a cube continuously. I will attach event handlers to stop rotation when mouse or finger touch/click event happens.
Friday, December 4, 2020
Qt / QML - a tool for modern application programming
Qt and QML are tools that can increase productivity of application development big time. Qt is a framework consisting of C++ libraries that can do almost everything conceivable as far as app development is concerned. It can even create android/ios applications.
Qt Creator is the IDE you can use to develop Qt/QML applications.
The best thing about Qt is that you can even use javascript like QML language to program the widgets on screen.
In fact you can write an entire application in QML without even touching C++.